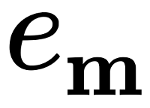Introduction¶
basicsusms is a package for computing structural sums and the effective conductivity of random composites.
The package forms a set of tools that can be divided into following submodules (see Fig. 1) presented in a bottom-up order. For theoretical details refer to Theory overview.
basicsums.weierstrass– incorporatesWeierstrassclass modeling Weierstrass \(\wp\) elliptic function and its derivative \(\wp'\) being foundation for Eisenstein functions \(E_k\) (\(k=2,3,\ldots\)). Instances are created based on given haflperiods of considered cell. Can be used as a standalone unit for calculations of \(\wp(z)\) and \(\wp'(z)\).basicsums.eisenstein– module for deriving mathematical objects being foundation of structural sums, i.e. Eisenstein-Rayleigh lattice sums \(S_k\) (\(k=2,3,\ldots\)) and Eisenstein functions \(E_k\) (\(k=2,3,\ldots\)) being algebraic combinations of \(\wp(z)\) and \(\wp'(z)\). Can be used as a standalone module for performing calculations of \(S_k\) and \(E_k(z)\). The module requiresbasicsums.weierstrassand is suitable for both numeric and symbolic calculations.basicsums.basic_sums– the key component of thebasicsumspackage, providing high level interface for computing structural sums. The unit cell is modelled byCellclass, of which instance determines and stores corresponding lattice sums and Eisenstein functions. For a particular cell, we can consider different configurations of points or disks. In order to compute structural sums for a given configuration, we create an instance ofBasicSums. At the time of creation, all required values of Eisenstein functions are computed and stored in form of matrices, before any sum is called (for more details, see [3] )basicsums.multi_indexes– module incorporating procedures for computing symbolic structure of consecutive multi-indexes of structural sums. The set of all structural sums is infinite, hence in applications we need its finite approximations. Functions implemented in the module, return a set of multi-indexes of structural sums that are sufficient to achieve a given polynomial approximation of the effective conductivity or a certain approximation of the structural sums feature vector.basicsums.conductivity– designed for an original application of basic sums: computing both purely symbolic and symbolic-numeric formulae for the effective conductivity of random 2D composites with circular non-overlapping inclusions.basicsums.preparation– providing functions that help the user to prepare data for the application of structural sums.basicsums.show_disks– this one-function module allows visualization of a system of disks in a given two-periodic cell with the help ofmatplotlib.
The package also incorporates a set of sample data that can be used alongside with tutorial from documentation.
Applications¶
Let us briefly present some applications of basic sums:
- description of random changes of microstructures [4]
- geometric features of data represented by distributions of disks [7], e.g. construction of the feature vector enables the immediate application of machine learning tools and data analysis techniques to random structures [2]
- basic sums as summary characteristics of point patterns (in preparation)
- Representative Volume Element Theory (RVE) [8]
- effective properties of 2D composite materials [6] [9] [10] [11]
- stir casting process [12]
- optimal packing problem [7] [5] [13]
- analysis of the collective behaviour of bacteria [14]
Target audience¶
Since structural sums may seem to be computationally and conceptually complex, the main goal of this package is to provide a high level of abstraction in calculations, hiding the underlying theory and algorithms. The ready-to-use package may be helpful for scientists from the field of computational materials science
The software may also attract the attention of researchers from other fields in order to experiment with structural sums as data analysis tools. Since structural sums have proven their value as carriers of geometrical information, the package can be applied to other types of data as long as the data is represented by distributions of non-overlapping disks, as wellas points, on the plane. The area of potential applications involves, for instance, plane objects frequently studied in biological and medical images.
Requirements¶
basicsusms runs under Python 3 and is written in pure Python. The package requires following scientific packages: numpy, matplotlib, and sympy.
A basic familiarity with Python is required.
Installation¶
Releases are hosted on PyPI, hence the easiest way to get basicsusms is to install it with pip:
pip install basicsums
You can also download the repository from Bitbucket
Once installed the package can be tested by running:
from basicsums.tests import test
test.run()
Function test.run() executes all doctests included in package’s docstrings as well as in test files residing in the tests submodule. The above code can be run directly in python interpreter. In order to get more detailed output specify the verbose=True keyword argument.
Contribution and citations¶
If you want to contribute, report an issue, need support or want to cooperate, contact the author with your questions.
If basicsusms contributes to your work, please acknowledge this fact by citing [1]. For underlying algorithms and methods, please mention [3] [5]. For the computational materials science theory based on structural sums, cite [6].
License¶
Copyright (c) 2017-2019, Wojciech Nawalaniec
basicsusms is an open source software made available under the New BSD License. For details see the LICENSE file.
References
| [1] |
|
| [2] |
|
| [3] | (1, 2)
|
| [4] |
|
| [5] | (1, 2)
|
| [6] | (1, 2)
|
| [7] | (1, 2)
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|