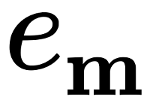Tutorial

This section is intended to make you familiar with the basicsums package for computing basic sums corresponding to distributions of disks or points. You can investigate all examples presented in this tutorial using interactive Jupyter notebook.

Hint

Some users may apply the %matplotlib inline magic function enabling a Matplotlib backend ensuring that outputs of plotting commands are displayed inline within the frontend.

Note

This section is under constant development. Its content will change and improve over time.

Let us present two simple scenarios of calculations:

• Assume that our goal is modelling random composite materials. First, we define the type of the unit cell; usually the hexagonal cell (rhombus with a \(\pi/3\) angle) or the unit square. Next, we generate a distribution of inclusions in the cell in torus topology. Finally, we compute structural sums and the effective conductivity with desired accuracy.
• On the other hand, assume that the user wants to analyze the data given by a two-dimensional array (i.e. an array of pairs). Note that structural sums operate on a subset of complex plane being a unit cell. In such a case, we have to prepare data to calculations. First, we convert data table to the array of complex numbers. Then we define a cell covering the data points; usually a unit rectangle determined by extreme values of points. Sometimes the boundary is known in advance, for instance, the area occupied by bacteria. Finally, we scale and translate both the data and the cell, so that the cell becomes a unit cell. We also scale radii, if given. Now we are ready to compute structural sums. The package is equipped with tools for such data preparation.

Contents:

• Computations of basic sums
  • Basic sums for identical disks
  • Disks of different radii
  • Computions of sequences of basic sums
  • Memoization and memory management
• Basic sums as summary characteristics
  • Example 1: Visualization of dynamic changes of the system
  • Example 2: Summary characteristics of distributions of disks
  • Example 3: Summary characteristics point patterns and regularization
• Effective conductivity of 2D random composites
  • Approximation of the symbolic formula
  • Numerical-symbolic calculations
• Appendix. Weierstrass \(\wp\) function and lattice sums
  • Eisenstein functions and Eisenstein-Rayleigh lattice sums
• Data preparation
  • Normalization
  • Regularization