Effective conductivity of 2D random composites

Note

This section is under constant development. Its content will change and improve over time.

Approximation of the symbolic formula

from basicsums.conductivity import coefficient_B, effective_conductivity

from sympy import symbols, pi, init_printing, expand, simplify
init_printing()
nu_s, rho_s = symbols('\u03BD \u03C1')

One can derive symbolic forms of terms of the coeeficient \(B_q\):

(coefficient_B(1, rho_s),
 coefficient_B(2, rho_s),
 coefficient_B(3, rho_s))

\[\left ( e(2) ρ, \quad e(2,2) ρ^{2}, \quad e(2,2,2) ρ^{3} - 2 e(3,3) ρ^{2}\right )\]

coefficient_B(4, rho_s)

\[e(2,2,2,2) ρ^{4} - 2 e(2,3,3) ρ^{3} - 2 e(3,3,2) ρ^{3} + 3 e(4,4) ρ^{2}\]

or sumbolic approximation of the effective conductivity series:

ec3 = effective_conductivity(nu=nu_s, q=3, rho=rho_s, pi=pi)
ec3

\[\frac{2 e(2) ν^{2} ρ^{2}}{\pi} + \frac{2 e(2,2) ν^{3} ρ^{3}}{\pi^{2}} + \frac{2 ν^{4} ρ \left(e(2,2,2) ρ^{3} - 2 e(3,3) ρ^{2}\right)}{\pi^{3}} + 2 ν ρ + 1\]

simplify(ec3)

\[\frac{2 \pi^{2} e(2) ν^{2} ρ^{2} + 2 \pi e(2,2) ν^{3} ρ^{3} + 2 ν^{4} ρ^{3} \left(e(2,2,2) ρ - 2 e(3,3)\right) + \pi^{3} \left(2 ν ρ + 1\right)}{\pi^{3}}\]

init_printing(pretty_print=False)

Numerical-symbolic calculations

Let us compute the symbolic-numerical approximation of the effective conductivity for a given configuration of disks. First, we import example data and define periods for the quare cell.

import numpy as np
from basicsums.examples import load_example01
A, r = load_example01()
N, nu = len(A), sum(r**2)*np.pi

w1 = 1
w2 = 1j

from basicsums.show_disks import show_disks
show_disks(A, r, w1, w2)

Let our approximation incorporate q=6 first coefficients \(B_q\) and compute values of required basic sums.

from basicsums.multi_indexes import sums_in_Gq_prime
from basicsums.basic_sums import Cell, BasicSums

q = 6
cell = Cell(w1, w2, q)

sums = sums_in_Gq_prime(q)
bso = BasicSums(A, cell, r)
results = bso.esums(sums, dict_output=True)
results

OrderedDict([((2,), (3.15438582262448-0.09180159581592136j)),
 ((2, 2), (11.757827037864901+5.82076609134674e-17j)),
 ((2, 2, 2), (43.07907709266533-1.7681300908296955j)),
 ((3, 3), (-3.557295937476818-7.450580596923828e-17j)),
 ((2, 2, 2, 2), (173.12898896402592-6.103515625e-15j)),
 ((3, 3, 2), (-10.80733726705118+1.833254246831019j)),
 ((4, 4), (7.9877213504124365-2.86102294921875e-16j)),
 ((2, 2, 2, 2, 2), (670.9285779378052-33.06492019934968j)),
 ((2, 3, 3, 2), (-50.034946200507406-2.9296875e-15j)),
 ((3, 3, 2, 2), (-42.96183376801067+6.393431885893068j)),
 ((3, 4, 3), (1.0336374840805849-1.3287290405279937j)),
 ((4, 4, 2), (25.69722017834029-1.0060002202097529j)),
 ((5, 5), (-16.913965412216037+2.44140625e-16j)),
 ((2, 2, 2, 2, 2, 2), (2801.2242234351697-2.05e-13j)),
 ((2, 3, 3, 2, 2), (-188.15069189815577+10.601837977710497j)),
 ((2, 4, 4, 2), (107.30650709107093-1.875e-15j)),
 ((3, 3, 2, 2, 2), (-155.34009851021497+41.19150453994921j)),
 ((3, 3, 3, 3), (39.59075459725217+2.5e-15j)),
 ((3, 4, 3, 2), (2.5510335185673747-4.11358081707618j)),
 ((4, 4, 2, 2), (103.60547850654284-2.0883152988130544j)),
 ((4, 5, 3), (0.9316723876832275+0.7154107026400275j)),
 ((5, 5, 2), (-54.55631093979708+1.40829410225262j)),
 ((6, 6), (26.34716019717142+1.5625e-16j))])

One can retrieve symbolic-numerical expression dependent on \(\rho\):

expr = effective_conductivity(nu=nu, q=q, rho=rho_s, results=results)
simplify(expr)

0.0217754043970236*ρ**7 - 1.59357393244145e-18*I*ρ**7 + 0.0470914953661529*ρ**6 - 0.00340488494383155*I*ρ**6 + 0.0891543602557013*ρ**5 - 1.98923904879937e-18*I*ρ**5 + 0.142246781888971*ρ**4 - 0.0084363108452773*I*ρ**4 + 0.249710501141987*ρ**3 + 1.09687688161722e-18*I*ρ**3 + 0.406649237832642*ρ**2 - 0.0118346489838408*I*ρ**2 + 0.9*ρ + 1.0

In order to compute a numerical value of the effective conductivity, we apply function effective_conductivity with \(\rho=1\).

rho = 1
effective_conductivity(nu, q, rho, results)

(2.8566277808824787-0.023675844772949668j)

One can also define function of parameter \(\rho\):

from sympy import lambdify
lam = lambdify((rho_s), expr, 'numpy')

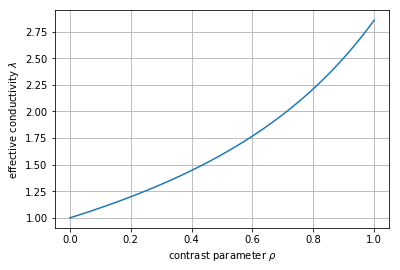
and plot \(\lambda(\rho)\):

import matplotlib.pyplot as plt

fig, ax = plt.subplots()

rho_array = np.linspace(0, 1, 100)
lam_array = np.real(lam(rho_array))

ax.plot(rho_array, lam_array,'-')
ax.set_xlabel(r'contrast parameter $\rho$')
ax.set_ylabel(r'effective conductivity $\lambda$')
ax.grid(True)
plt.show()