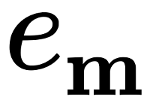Appendix. Weierstrass \(\wp\) function and lattice sums

Note

This section is under constant development. Its content will change and improve over time.

import numpy as np

from basicsums.weierstrass import Weierstrass
from basicsums.eisenstein import E_numeric

w1 = 1
w2 = 1j

wp = Weierstrass(w1/2, w2/2)

wp.wp(0.1+0.1j) # Weierstrass P function

(-4.440892098500626e-15-49.81116546459035j)

wp.wpp(0.1+0.1j) # derivative of th Weierstrass P function

(501.88358442957417+501.8835844295741j)

Eisenstein functions and Eisenstein-Rayleigh lattice sums

from basicsums.eisenstein import lattice_sums

S = lattice_sums(w1, w2, 6)

S[2]

3.1415926535897927

from basicsums.eisenstein import E

E(3), E(4)

(-P'(z)/2, P(z)**2 - 5*S(4))

E(10)

(8*P(z)**5 - 76*P(z)**3*S(4) + 5*P(z)**2*P'(z)**2 + 180*P(z)*S(4)**2 - 11*P'(z)**2*S(4))/28

from basicsums.eisenstein import E_numeric

E2 = E_numeric(2, w1, w2)
E2(0.1 + 0.5j)

(-2.8498259468658538-6.84841378126949e-16j)

E3 = E_numeric(3, w1, w2)
E3(0.1 + 0.5j)

(-8.25402443117664+3.1086244689504383e-15j)

E4 = E_numeric(4, w1, w2)
E4(0.1 + 0.5j)

(20.14103683511636+8.206342742542959e-15j)