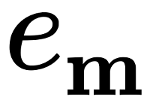basicsums package

Submodules

basicsums.basic_sums module

A module for computing basic sums. The main part of the basicsums package.

Available classes:

  • Cell: represents a two-periodic cell
  • BasicSums: class of objects tackling computations of basic sums.

The BasicSums class is equipped with methods and algorithms developed in [1] . Such algorithms are build around products of matrices of values of Eisenstein functions.

References:

[1](1, 2) W.Nawalaniec, Efficient computation of basic sums for random polydispersed composites, Computational and Applied Mathematics, DOI: 10.1007/s40314-017-0449-6.
class basicsums.basic_sums.BasicSums(A, cell, r=None, eisenstein_indexes=None)

Bases: object

Represents an object tackling computations of basic sums for a given centers of disks.

Parameters:

A : NumPy array of complex numbers
Array of centers of disks.
cell : Cell object
An object corresponging to considered cell.
r : NumPy array of floats (optional)
Array of radii corresponding to disks. If provided, the centers of A are considered to be the centers of disks of different radii, therwise the equal disks are assumed.
eisenstein_indexes : sequence of integers (default None)
A sequence of indexes of Eisenstein Functions required in computations. Note that the indexes should not exceed \(q\). If not provided, the default range is (2, 3, …, cell.q).

Attributes:

eis : dictionary
A dictionary of matrices computed for Eisenstein functions, based on an array of centers \(A\). Matrices are computed for considered indexes of Eisenstein functions.

Examples:

>>> w1, w2 = 1, 1j
>>> cell = Cell(w1, w2, q=3)
>>> A = np.random.rand(10, 2).dot(np.array([1, 1j]))-(w1+w2)/2
>>> bso = BasicSums(A, cell)
>>> e2 = bso.esum(2)
>>> # Compare the value of e2 with the naive approach:
>>> from basicsums.eisenstein import E_numeric
>>> E2 = E_numeric(2, w1, w2)
>>> e2naive = 1/len(A)**2 * sum(E2(ak0-ak1) for ak0 in A for ak1 in A)
>>> np.isclose(e2, e2naive)
True
clear_cache()

Clears the dictionary with cached vector representations of sums.

It takes effect only if a nonlocal cache is applied, see nonlocal_cache argument of esums().

esum(*tup)

Return single basic sum for multi-index given as arguments, e.g. \(\mathbf{esum}(p_1, p_2,p_3)\) computes \(e_{p_1, p_2,p_3}\).

esums(multi_indexes, dict_output=False, maxsize=None, cache_only=None, nonlocal_cache=False)

Return basic sums for a given indexes from multi-indexes.

Parameters:

multi_indexes : sequence
A sequence of sequences representing multi-indexes, e.g. passing following list of tuples [(2, 2), (3, 3, 2), (4, 4)] results in computing list of sums \(e_{2, 2}\), \(e_{3, 3, 2}\), \(e_{4, 4}\).
dict_output : boolean (default False)
If False, return corresponding values of sums as NumPy array, otherwise as OrderedDict, where the tuples are associated with values of basic sums.
maxsize : integer (default None)
Determines maximal number of vector representations of intermediate sums cached during computations. By default all intermediate results are cached or only those provided by cache_only argument.
cache_only : sequence (default None)
A sequence of sequences representing multi-indexes of sums which should only be cached during computations. By default all intermediate results are cached. For more details see documentation.
nonlocal_cache : boolean (default False)
By the default, the cache is built as a local variable hence it exists oly during a function call. If True, the cache is maintained as a object’s attribute and persists between independent method calls. Takes no effect if nonlocal cache is built already. For more details see documentation.
class basicsums.basic_sums.Cell(w1, w2, q)

Bases: object

Represents a two-priodic unit cell.

For details see Basic sums and the effective conductivity of composites. An instance stores both lattice sums \(S_n\) and Eisentein Functions \(E_n\) corresponding to considered unit cell.

Parameters:

w1, w2 : complex numbers
Periods of a unit cell.
q : integer
Symbolic precision of considerations, i.e. maximal order of Eisenstein functions \(E_n\) used in computations.

Attributes:

wp : Weierstrass class object
An instance of the Weierstrass class corresponding to considered periodic cell.
wp2, wpp2 : callable
Vectorized functions \(\wp\) and \(\wp'\) respectively.
S : array of floats
An array of lattice sums \(S_n\) (\(n=2, 3, 4, \ldots, \max(q, 6)\)) (see Weierstrass \wp and Eisenstein functions).
eisenstein_funs : dictionary
Dictionary of Eisenstein functions corresponding to a cell. The dictionary contains pairs of the form {order \(n\): function \(E_n\)}. Each function is a function of two variables, hence in order to compute value \(E_n\) for a given \(z\), on should pass \(\wp(z)\) and \(\wp'(z)\) as arguments.
eis_matrices(A, eisenstein_indexes)

Return a dictionary of matrices for Eisenstein functions computed for a given array of centres \(A\).

Parameters:

A : NumPy array of complex numbers
Array of centers of disks.
eisenstein_indexes : sequence of integers
A sequence of indexes of Eisenstein Functions required in computations. Note that the indexes should not exceed \(q\).

Returns:

m : dictionary
The dictionary contains pairs of the form {order \(n\): NumPy array for a given \(E_n\)} (see [1] ).

basicsums.conductivity module

A module for computing the effective conductivity of random composite materials modelled by non-overlapping disks.

Available functions:

The module is suitable for both symbolic and numeric computations, as well as for mixed symbolic-numerical results. For more details on theory, see Basic sums and the effective conductivity of composites.

basicsums.conductivity.coefficient_B(q, rho, results=None)

Return a coefficient \(B_q\) of series \(\lambda\)

Parameters:

q: integer
An order \(q\) of the coefficient \(B_q\).
rho: number or symbol
Represents constant parameter \(\rho\).
results: None or a dictionary (default None)
Dictionary of pairs: tuple representing multi-index with corresponding numerical value of basic sum. The dictionary should provide pairs for every basic sums involved in \(B_q\). When the default value is used, basic sums are exoressed symbolically.
basicsums.conductivity.effective_conductivity(nu, q, rho, results=None, pi=3.141592653589793)

Return approximation of the effective conductivity series \(\lambda\).

Parameters:

nu: number or symbol
Represents concentration of disks.
q: integer
An order \(q\) of the coefficient \(B_q\).
rho: number or symbol
Represents constant parameter \(\rho\). Can be given in a symbolic form.
results: None or dictionary (default None)
Dictionary of pairs: tuple representing multi-index and the corresponding numerical value of basic sum. The dictionary should provide pairs for every basic sums involved in \(B_q\). When the default value is used, basic sums are expressed symbolically.
pi: number or symbol (default numerical value of \(\pi\))
Represents \(\pi\). Can be given in a symbolic form.

basicsums.eisenstein module

A module for computing symbolic forms and numerical values of the Eisenstein functions \(E_n\) and the Eisenstein lattice sums \(S_n\).

Available functions:

  • E(): computes a symbolic representation of Eisenstein function \(E_n\).
  • E_numeric(): produces the Eisenstein function \(E_n\) suitable for numerical computations.
  • lattice_sums(): returns an array of lattice sums \(S_n\).
  • eisenstein_funs(): returns a dictionary of Eisenstein functions.

The definition of the Eisenstein functions \(E_n\) is built on the Weierstrass \(\wp\) function and its derivative. For more details on theory, see Eisenstein-Rayleigh lattice sums and Weierstrass \wp and Eisenstein functions.

basicsums.eisenstein.E(n)

Compute a symbolic representation of Eisenstein function of order \(n\).

The function requires the sympy package in order to perform symbolic manipulations. For numerical calculations use E_numeric() instead.

Parameters:

n : integer (\(n \geq 2\))
The order \(n\) of the Eisenstein function \(E_n\).
basicsums.eisenstein.E_numeric(n, w1, w2)

Return numeric Eisenstein function \(E_n\) for a given periods w1, w2.

0ne can directly compute the value \(E_n\).

Parameters:

n : integer (\(n \geq 2\))
The order \(n\) of the Eisenstein function \(E_n\).
w1, w2 : complex numbers
The periods of Eisenstein function \(E_n\).

Examples:

>>> E2 = E_numeric(2, 1, 1j) # square unit cell
>>> np.isclose(E2(0), np.pi)
True
class basicsums.eisenstein.P

Bases: sympy.core.function.AppliedUndef

default_assumptions = {}
basicsums.eisenstein.Pp

alias of P'

class basicsums.eisenstein.S

Bases: sympy.core.function.AppliedUndef

default_assumptions = {}
basicsums.eisenstein.eisenstein_funs(nmax, S2, S4, S6)

Return a dictionary with first nmax vectorized Eisenstein functions. The procedure is used by objects of basic_sums module.

The dictionary contains pairs of the form {order \(n\): function \(E_n\)}. Each function is a function of two variables, hence in order to compute value \(E_n\) for a given \(z\), one should pass, respectively, \(\wp(z)\) and \(\wp'(z)\) as arguments.

Parameters:

nmax : integer
Maximal value of the order of considered Eisenstein functions \(E_n\).
S2, S4, S6 : real numbers
The Eisenstein lattice sums for a given periodic cell. The sums can be calculated via lattice_sums() function.
basicsums.eisenstein.lattice_sums(w1, w2, qmax, inf=100)

Return an array of Eisenstein_Rayleigh lattice sums \(S_n\) up to \(S_{qmax}\).

Parameters:

w1, w2 : complex numbers
The periods of Eisenstein function \(E_n\).
qmax : integer
Maximal order of considered sums.
inf : integer (default 100)
Number of terms of partial sums approximating infinite sums \(S_n\), see Eisenstein-Rayleigh lattice sums.

basicsums.multi_indexes module

A module for computing a symbolic approximation of the set \(\mathcal M_e\) consisting of all basic sums included in series \(\lambda\) (2) described in Basic sums and the effective conductivity of composites of online documentation.

Available functions:

  • sums_in_Bq(): returns list of multi-indexes of basic sums included in the coefficient \(B_q\).
  • sums_in_Gq(): returns list of multi-indexes of basic sums included in the set \(G_q\).
  • sums_in_Gq_prime(): returns list of multi-indexes of basic sums included in the set \(G_q'\).

The sums_in_Bq(), sums_in_Gq(), and sums_in_Bq() functions are equipped with methods and algorithms developed in [2] (for the definition of \(B_q\), \(G_q\), and \(G_q'\) sets see the paper as well as Approximation of Me and symbolic precision section of the online documentations).

References:

[2](1, 2, 3)
  1. Nawalaniec, Algorithms for computing symbolic representations of basic e–sums and their application to composites, Journal of Symbolic Computation, Vol. 74, 328-345, 2016.
basicsums.multi_indexes.sums_in_Bq

Return the list of multi-indexes of basic sums included in the coefficient \(B_q\) of the series \(\lambda\) (2). The list is created recursively via (1) (see the online documentation or [2] for more details).

Parameters:

q : integer
An order of basic sums, e.g. passing \(q=4\) results in returning the following list of multi-indexes: [(2, 2, 2, 2), (2, 3, 3), (3, 3, 2), (4, 4)].
>>> sums_in_Bq(4)
[(2, 2, 2, 2), (2, 3, 3), (3, 3, 2), (4, 4)]
basicsums.multi_indexes.sums_in_Gq

Return the list of multi-indexes of independent basic sums included in the coefficient \(B_q\). The list is created from \(B_q\) by reduction of the mirror sums (see the online documentation or [2] for more details).

Parameters:

q : integer
An order of basic sums, e.g. passing \(q=4\) results in returning the following list of multi-indexes: [(2, 2, 2, 2), (3, 3, 2), (4, 4)].
>>> sums_in_Gq(4)
[(2, 2, 2, 2), (3, 3, 2), (4, 4)]
basicsums.multi_indexes.sums_in_Gq_prime(q)

Return the list of multi-indexes of independent basic sums included in the set \(G_q'\) considered as an approximation of the set \(\mathcal M_e\) consistsing of indexes of all basic sums included in the series \(\lambda\) (2) described in Basic sums and the effective conductivity of composites of online documentation.

Parameters:

q : integer
An order of basic sums, e.g. passing \(q=4\) results in returning the following list of multi-indexes: [(2,), (2, 2), (2, 2, 2), (3, 3), (2, 2, 2, 2), (3, 3, 2), (4, 4)].
>>> sums_in_Gq_prime(4)
[(2,), (2, 2), (2, 2, 2), (3, 3), (2, 2, 2, 2), (3, 3, 2), (4, 4)]

basicsums.preparation module

A module providing simple functions that can be used to prepare data for application of basic sums.

Available functions:

basicsums.preparation.normalize_cell_periods(w1, w2)

Returns scaled periods forming unit parallelogram and the corresponding scale factor a.

Parameters:

w1, w2 : complex numbers
Periods of considered non-unit cell.
>>> from cmath import isclose, exp, pi, sqrt
>>> w1, w2 = 2, 1j # rectangular cell 2x1
>>> w1, w2, a = normalize_cell_periods(w1, w2)
>>> area = w1*w2.imag # the area of the parallelogram
>>> isclose(area, 1)
True
>>> w1, w2 = 1, 1*exp(1j*pi/3) # non-unit hexagonal cell
>>> w1_temp = w1
>>> w1, w2, a = normalize_cell_periods(w1, w2)
>>> isclose(w1, sqrt(2)/(3**(1/4)))
True
>>> isclose(w2, w1*exp(1j*pi/3))
True
>>> isclose(a*w1_temp, w1)
True
basicsums.preparation.normalize_data(data, W=None, H=None, return_factor=None)

Returns scaled data so that the resulting data is bounded by a unit rectangle.

Parameters:

data : NumPy array of complex numbers
Array of centers of disks.
W, H : floats
Numbers representing, respectively, the width and the height of the original box bounding the data. If not provided, they are computed based on extremal values of real and imaginary parts of data points.
return_factor: boolean
If true, returns scale factor as fourth element of resulting tuple.
>>> import numpy as np
>>> data = 5*np.random.random(100000) + 3j*np.random.random(100000)
>>> w1, w2, data = normalize_data(data, 5, 3)
>>> np.isclose(w1*(w2.imag), 1)
True
>>> min(data.real) >= -w1/2, max(data.real) <= w1/2
(True, True)
>>> min(data.imag) >= -w2.imag/2, max(data.imag) <= w2.imag/2
(True, True)
basicsums.preparation.real_array_to_complex(arr)

Returns array of complex numbers of the form \(x+iy\) being a represantation of real 2D coordinates \((x, y)\)

>>> data = np.array([[-1, 1], [2, -2]])
>>> real_array_to_complex(data)
array([-1.+1.j,  2.-2.j])
basicsums.preparation.regularized_radii(A, w1, w2)

Returns radii \(r\) for a given sequence of points \(A\). The radii \(r_j\) for a given point \(a_j\) is computed as the half of the minimum of distances from \(a_j\) to the remaining points and the points from neighboring cells (i.e. distance in torous topology is considered).

>>> w1, w2 = 1, 1j # rectangular cell 1x1
>>> A = np.array([-0.3+0.5j, 0.3+0.5j])
>>> R = regularized_radii(A, w1, w2)
>>> np.all(np.isclose(R, np.array([0.2, 0.2])))
True

basicsums.show_disks module

A module for drawing a sample of a distribution of disks in a given two-periodic cell

Available functions:

basicsums.show_disks.show_disks(disks, r, w1, w2, neighbs=True, figsize=None)

Plots a matplotlib figure with an illustration of a set of disks distributed in a two-periodic cell.

Parameters:

disks : NumPy array of complex numbers
Array of centres of disks.
r : NumPy array of floats
Array of radii corresponding to disks.
w1, w2 : complex numbers
Periods of the considered cell.
neighbs : boolean (default True)
If true, it plots the neighbouring cells with disks. Otherwise, only the (0,0)th cell contains disks.
figsize: tuple of integers, optional, default: None
width, height in inches. If not provided, defaults to rcParams["figure.figsize"]

basicsums.weierstrass module

Module for computing values of Weierstrass \(\wp\) and \(\wp'\) functions.

Available classes:

  • Weierstrass: represents functions \(\wp\) and \(\wp'\) for a given halfperiods.

Since the functions \(\wp\), \(\wp'\) are doubly periodic, the Weierstrass uses inner helper function in order to bring arguments to the base (0,0)th cell. This constitutes in a better convergence.

class basicsums.weierstrass.Weierstrass(hw1, hw2, inf=20, inf_eta=10)

Bases: object

Represents Weierstrass \(\wp\) function and its derivative for given haflperiods hw1, hw2 (see [3], Table X, p. 204, Weierstrass \wp and Eisenstein functions and Tutorial).

Parameters:

hw1, hw2 : complex numbers
Halfperiods of Weierstrass \(\wp\) function.
inf : integer (default 20)
Number of terms of an approximation of the series expansion of \(\wp\) and \(\wp'\) functions (see [3], Table X, p. 204 ).
inf_eta : integer (default 10)
Number of terms of series approximation of constant \(\eta\) involved in computations (see [3], Table X, p. 204). It was observed that the default value 10 gives good approximations.

References:

[3](1, 2, 3)
    1. Akhiezer, Elements of the Theory of Elliptic Functions, American Mathematical Society, 1990.
wp(u)

Return the value \(\wp(u)\) of the Weierstrass \(\wp\) function for a given complex number \(u\).

wpp(u)

Return the value \(\wp'(u)\) of the derivative of Weierstrass \(\wp\) function for a given complex number \(u\).

Module contents

A package for computing structural sums and the effective conductivity of random composites

Structural sums (also known as basic sums) are mathematical objects originating from the computational materials science, considered to form a set of geometric features of data represented by points or disks on the plane.

See the structural sums overview, package description, tutorials, example usage and API reference on http://basicsums.bitbucket.io