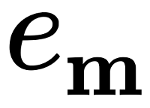Weierstrass \(\wp\) and Eisenstein functions¶
The Eisenstein functions \(E_n(z)\) (\(n=2,3,\ldots\)) and the Weierstrass function \(\wp(z)\) are related by the identities
where \(z\neq 0\) and \(S_2\) is a constant. It follows from the elliptic function theory [1] and from [2] that
Here \(S_2\) and \(S_4\) stand for lattice sums defined in Appendix [eisenFun]. Thus each function \(E_n(z)\) is an algebraic combination of \(\wp(z)\) and \(\wp(z)'\). One can implement both functions \(\wp(z)\) and \(\wp(z)'\) via approximation of the series expansion (see [1], Table X, p. 204). Dependencies (1) and (2) be implemented in any Computer Algebra System, in order to calculate the symbolic representations of \(E_n(z)\).Hence, to determine matrices for Eisenstein functions combined in a given basic sum, it is sufficient to perform a set of algebraic operations on the base matrices \(C_\wp\) and \(C_\wp'\). In addition, it will be convenient to define the value of \(\wp\) and \(\wp'\) at the origin as zero. For the definition of \(E_n(z)\) at the origin, see section on lattice sums.
References
| [1] | (1, 2)
|
| [2] |
|