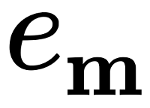Geometric parameters

Why the basic sums describe geometry?

Let us briefly describe the connection of basic sums with the geometry of a set of disks randomly distributed on the plane, following [2].

Note that basic sums originate from the theory of composites (see Basic sums and the effective conductivity of composites). Microstructure of composites and its dynamic changes depend on geometrical parameters. A proper choice of these parameters and a possibility of their effective computations can give a description of the corresponding local physical fields and of the macroscopic properties of composites. The mathematical framework for searching the key geometrical parameters to relate geometry and physics seems to be one of the most important problems of the mathematical modelling in modern physics, in particular, in material sciences.

The fundamental problem of composites consists in construction of the homogenization operator \(\mathcal H: G \to M\), where \(G\) stands for microstructure (geometry) and \(M\) for the macroscopic physical constants. Local physical parameters are considered here as parameters of the operator \(\mathcal H\). Randomness is an important feature of composites, hence the set \(G\) can be endowed with a probabilistic structure. A regular location of inclusions can be considered as an event in the probabilistic space of possible geometric configurations. By the homogenization operator \(\mathcal H\) we mean a method to compute the macroscopic constants \(M\) existence of which are justified under some natural conditions on \(G\) due to the traditional homogenization theory . The key point is a precise and convenient description of the geometrical set \(G\) which can be given, for instance, as a set of images.

The approach developped in [2] proposes the choice of the geometric parameters as the following set of basic sums:

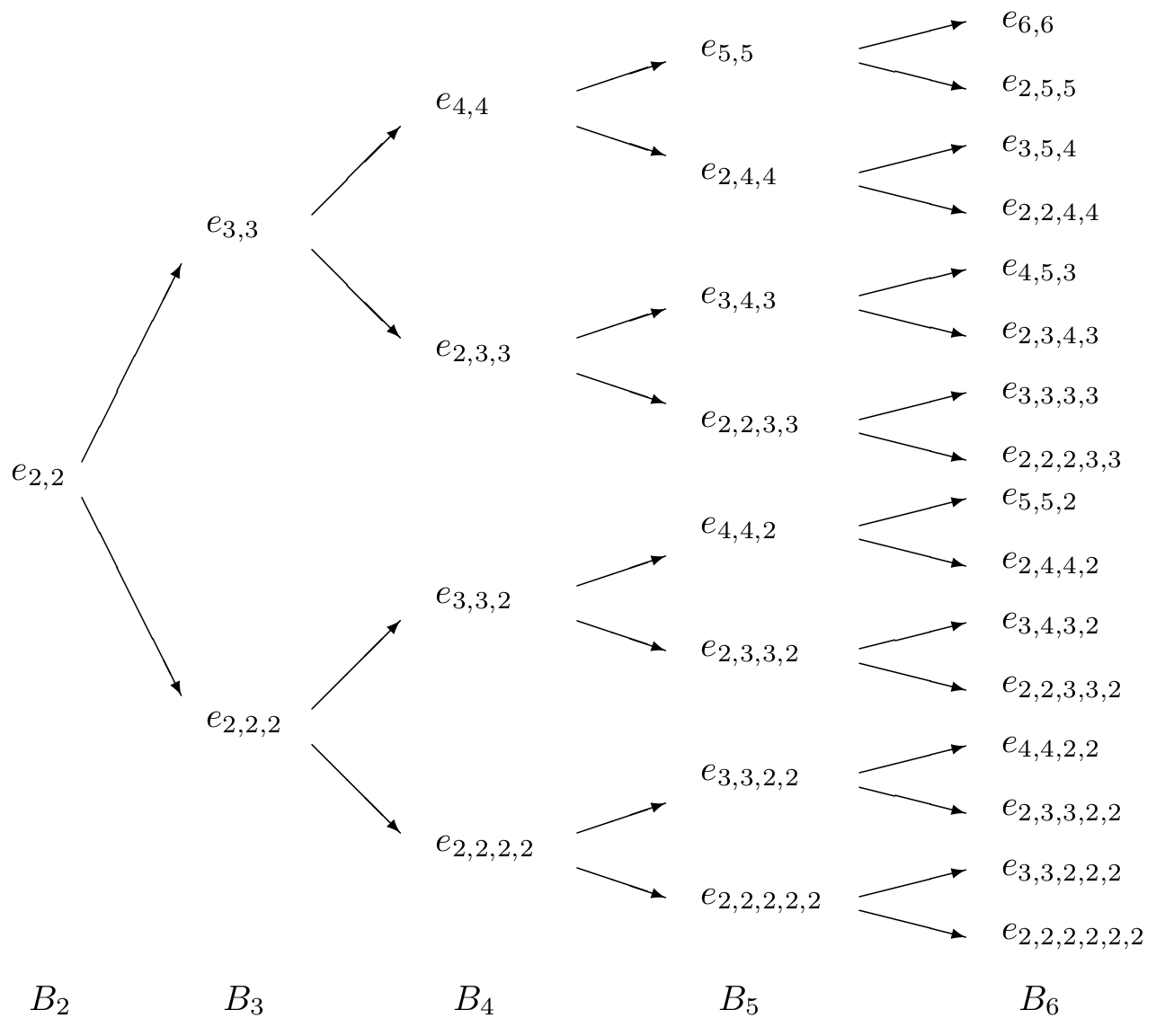
\(G =\{ e_{\mathbf m}, \;\mathbf m \in \mathcal M_e\}\) where the set \(\mathcal M_e\) consists of all basic sums included in series \(\lambda\) (2) described in Basic sums and the effective conductivity of composites. hence, following theorem, the set \(\mathcal M_e\) can be recursively introduced by the rules:

(1)\[\begin{split}\label{eq:2.18} \begin{array}{lll} 1.&(2), (2,2)\in {\mathcal M_e}; & \\ \\ 2.&If \ (m_{1},\ldots,m_{q})\in{\mathcal M_e} \ and\ q>1, \ then \\ \\ &(2,m_{1},\ldots,m_{q}),(m_{1}+1,m_{2}+1,m_{3},\ldots,m_{q})\in{\mathcal M_e}. \end{array}\end{split}\]

The elements \(e_{\mathbf m}\) can be treated as weighted moments (integrals over the cell) of the \(n\) correlation functions \(S_n(\mathbf x_1, \mathbf x_2, \ldots, \mathbf x_n),\; n \in \mathbb N \}\) (for more details on correlation functions, see [4]) . Use of \(e_{\mathbf m}\) allows to avoid huge computation of the correlation functions and compute implicitly their weighted moments of high orders.

As the results of [1] and [2] show, the set \(G\) can be applied in describing geometry of disks randomly distributed on the plane. This approach is rigorously justified for non-overlapping equal disks . Any geometrical configuration of two-phase composites can be approximated by disks. This extends applications of the basic sums to general 2D structures.

The structure of the set \(\mathcal M_e\) has teh graphical form (see Fig. 1).

Fig. 1 Graph of basic e-sums of orders \(q = 2, 3, 4, 5, 6\) .

Approximation of \(\mathcal M_e\) and symbolic precision

The set \(\mathcal M_e\) discussed above is infinite, hence in applications we need its approximation.

Note that the coefficients \(B_q\) involve dependent sums. Indeed, the following lemma, describes a correspondence between so-called mirror basic sums.

Lemma [3] Let \(\alpha=\sum^n_{j=1}p_j\). Then

\[\label{eq:mirr1} \begin{array}{lll} e^{\nu_0,\nu_1,\nu_2,\ldots,\nu_n}_{p_1,p_2,p_3,\ldots,p_n}=(-1)^\alpha\mathbf{C}^{n+1}e^{\nu_n,\nu_{n-1},\nu_{n-2},\ldots,\nu_1}_{p_n,p_{n-1},p_{q-2},\ldots,p_1}. \end{array}\]

As it turns out, nearly half of terms in symbolic representation of the coefficient \(B_q\) reduces. One can applied the lemma in order to consider independent sums only. Let \(M_q\) be the set of all basic sums of order \(q\). By the virtue of relations (1), consecutive sets \(M_q\) can be generated iteratively as follows:

\[\begin{split}\begin{array}{l} M_1 = \{e_{2}\}, \quad M_2 = \{e_{2, 2}\}, \quad M_3 = \{e_{2, 2, 2}, e_{3, 3}\}\\ M_4 = \{e_{2, 2, 2, 2}, e_{2, 3, 3}, e_{3, 3, 2}, e_{4, 4} \}\\ M_5 = \{e_{2, 2, 2, 2, 2}, e_{2, 2, 3, 3}, e_{2, 3, 3, 2}, e_{2, 4, 4}, e_{3, 3, 2, 2}, e_{3, 4, 3}, e_{4, 4, 2}, e_{5, 5} \}.\\ M_6 = \{e_{2, 2, 2, 2, 2, 2}, e_{2, 2, 2, 3, 3}, e_{2, 2, 3, 3, 2}, e_{2, 2, 4, 4}, e_{2, 3, 3, 2, 2}, e_{2, 3, 4, 3}, e_{2, 4, 4, 2}, e_{2, 5, 5},\\ \qquad\qquad\qquad e_{3, 3, 2, 2, 2}, e_{3, 3, 3, 3}, e_{3, 4, 3, 2}, e_{3, 5, 4}, e_{4, 4, 2, 2}, e_{4, 5, 3}, e_{5, 5, 2}, e_{6, 6} \}.\\ \end{array}\end{split}\]

Let \(G_q\) denote subset of \(M_q\), containing independent sums only. For instance, the set \(G_6\) takes the following form:

\[\begin{split}\begin{array}{l} G_6 = \{e_{2, 2, 2, 2, 2, 2}, e_{2, 3, 3, 2, 2},e_{2, 4, 4, 2}, e_{3, 3, 2, 2, 2}, e_{3, 3, 3, 3}, e_{3, 4, 3, 2}, e_{4, 4, 2, 2},\\ \qquad\qquad\qquad e_{4, 5, 3}, e_{5, 5, 2}, e_{6, 6} \}. \end{array}\end{split}\]

Whether we consider basic sums as components of the effective conductivity formula  or the set of geometric parameters , the key problem is to determine values of basic sums of several initial orders. For example, the aproximation of series (2) \(\lambda\) as the polynomial of degree \(q\), requires to compute all elements of \(G'_q = \bigcup_{j=1}^q G_j\).

Hence, we consider the sets \(G'_q\), \(q=1, 2, 3, \ldots\) as consecutive approximations of the set \(\mathcal M_e\).

The term of symbolic precision was introduced in [2] . We say that symbolic precision \(O(\nu^{q})\) is used, as long as basic sums from \(G'_q\) are under consideration.

References

[1]	Nawalaniec, Sumy bazowe i ich zastosowanie do symulacji losowych struktur, PhD dissertation, Gliwice, 2015.

[2]	(1, 2, 3, 4) Mityushev, W. Nawalaniec, Basic sums and their random dynamic changes in description of microstructure of 2D composites, Computational Materials Science, Vol. 97, 64–74, 2015.

[3]	Nawalaniec, Algorithms for computing symbolic representations of basic e–sums and their application to composites, Journal of Symbolic Computation, Vol. 74, 328-345, 2016.

[4]	Torquato, Random Heterogeneous Materials: Microstructure and Macroscopic Properties, Springer-Verlag, 2002.