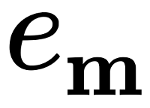Eisenstein-Rayleigh lattice sums

Consider the lattice \(\mathcal{Q}\) (see section [background]). For definiteness, it is assumed that \(\textrm{Im}\;\tau>0\), where \(\tau =\omega _{2}/\omega _{1}\). The Eisenstein summation is defined by the iterative sum

(1)\[\sum_{m_{1},m_{2}}=\lim_{N\rightarrow \infty }\sum_{m_{2}=-N}^{N}\left( \lim_{M\rightarrow \infty }\sum_{m_{1}=-M}^{M}\right) . \label{2.2}\]

The lattice sums are introduced as follows

(2)\[S_{n}:=\sum_{m_{1},m_{2}}\;^{\prime }(m_{1}\omega _{1}+m_{2}\omega _{2})^{-n} \quad (n=2,3,\ldots), \label{2.1}\]

where the prime means that \(m_{1}\) and \(m_{2}\) run over all integer numbers as in (1) except the pair \((m_{1},m_{2})=(0,0)\). The sum \(S_{2}\) is conditionally convergent and understood in the sense of the Eisenstein summation (1). Though the rest sums (2) converge absolutely, the direct computations by (2) are problematic because of their slow convergence. The sum \(S_{2}\) can be computed by a quick formula [2] :

\[S_{2}= \left( \frac{\pi }{\omega _{1}}\right) ^{2}\left( \frac{1}{3}-8\sum_{m=1}^{\infty }\frac{mq^{2m}}{1-q^{2m}}\right) ,\text{ where }q=\exp \left( \pi i\tau \right). \label{2.3}\]

It is known that \(S_{n}=0\) for an odd \(n\). For an even \(n\), the sums (2) can be easily computed through the rapidly convergent infinite sums [2] :

\[\begin{split}\begin{aligned} S_{4}=\frac{1}{60}\left( \frac{\pi }{\omega _{1}}\right) ^{4}\left( \frac{4}{3}+320\sum_{m=1}^{\infty }\frac{m^{3}q^{2m}}{1-q^{2m}}\right) ,\; \label{2.5} \\ S_{6}=\frac{1}{140} \left( \frac{\pi }{\omega _{1}}\right) ^{6}\left( \frac{8}{27}-\frac{448}{3}\sum_{m=1}^{\infty }\frac{m^{5}q^{2m}}{1-q^{2m}}\right).\end{aligned}\end{split}\]

The sums \(S_{2n}\) (\(n\geq 4\)) are calculated by the recurrence formula  [2] :

\[S_{2n}=\frac{3}{\left( 2n+1\right) \left( 2n-1\right) \left( n-3\right) }\sum_{m=2}^{n-2}\left( 2m-1\right) \left( 2n-2m-1\right) S_{2m}S_{2(n-m)}. \label{2.7}\]

The Eisenstein series are defined as follows [1]

\[E_{n}(z):=\sum_{m_{1},m_{2}}(z-m_{1}\omega _{1}-m_{2}\omega _{2})^{-n}\,,\;n=2,3,...\;. \label{2.8}\]

Each of the functions ([2.8]) is doubly periodic and has a pole of order \(n\) at \(z=0\). Further, it is convenient to define the value of \(E_{n}(z)\) at the origin as \(E_{n}(0):=S_{n}.\)

References

[1]	Weil, Elliptic Functions According to Eisenstein and Kronecker, Springer-Verlag Berlin Heidelberg, 1976

[2]	(1, 2, 3) Mityushev, E. Pesetskaya, S. V. Rogosin, Analytical Methods for Heat Conduction in Composites and Porous Media, in Cellular and Porous Materials: Thermal Properties Simulation and Prediction, A. Öchsner, G. E. Murch, M. J. S. de Lemos, eds., Wiley, 121-164, 2008.